minden·ki·jön – 16. nap
Téglavár · Teák szigete II. | Patak, vasút, ösvény · Ugráljunk!
A héten ez az utolsó levelünk, újra egy hosszabb pihenő következik. Többször felmerült, hogy lehet-e korábbi feladatok megoldásait beküldeni, erre a válasz igen, sőt, mindenkit biztatunk is erre.
Szubjektív módon ki is emelünk néhány feladatot: Egy nap általában az első feladatra érkezik több megoldás, ez alól két kivétel volt eddig. A széf kinyitása népszerűbb volt, mint a reggeli kávés feladat. A másik minket jobban meglepett, több megoldást kaptunk a szaloncukros feladatra, mint a Janus arcú légióra. Kiemelkedően népszerű volt a π-raktár dobozai. Az egyre jobb kérdések feladatnál még nem érkezett megoldás az általános esetre (mi sem látjuk ezt).
Jó pihenést és gondolkozást kívánunk!
Téglavár
Régóta tudták, hogy Téglavár falu határában valamikor egy vár állott (most kőhalom). Egy kapitány levelében megemlíti, hogy „a földszintes négyszegletű épület téglalap alaprajzú, és belsejében mindössze hat négyzet alakú helyiség van”. A közelmúltban a régészeti kutatás is eredménnyel járt: sikerült a falak alapjainak bizonyos részeit feltárni, annyit, amennyi az ásatási jegyzőkönyv mellékelt vázlatán látható. A maradványokból egy helyiség teljes egészében kirajzolódik, falai 10 láb hosszúak – a középvonaluk mentén mérve. Minthogy a falvastagság mindenütt nagyjából azonos, tekintsünk el tőle, a falakat a középvonalaikkal adjuk meg.
Rajzoljuk meg a vár teljes alaprajzát, és határozzuk meg (lábban) a méreteit Hány láb a vár rövidebbik oldalának hossza?
Teák szigete II. (**)
Most újra egy teákat termesztő kör alakú szigeten járunk, de itt négyféle teát termesztenek. A következőket tudjuk a teaföldekről:
Mind a négy teaföld területe egyenlő, negyede a teljes sziget területének.
Mind a négy teaföld kerülete megegyezik a sziget kerületével.
Fajtánként összefüggő területet alkotnak a termőföldek.
Csodás látványt is nyújt a sziget az ültetvényekkel, a teák csomagolásán logóként köszön vissza ez a sajátos elrendezés :)
Rajzolj egy felosztást, ami eleget tesz a feltételeknek! Sokféle konstrukció létezik, keress minél egyszerűbben lerajzolhatót! Ha szívesen rajzolsz ilyet, örülünk, ha elküldöd nekünk, de akár szövegesen is leírhatod. Tudsz olyan felosztást (is) rajzolni, ahol nem egyforma alakú a négy teaföld?
Patak, vasút, ösvény
Egy ösvény mellett végig kanyarog egy patak és egy vasútvonal is. A túra elején tőlünk balra van a patak, és a pataktól balra a sín. Összesen nyolcszor keresztezzük a patakot és ötször a sínt. Meg lehet-e ez alapján állapítani, hogy a túra végén milyen sorrendben helyezkedik el a patak, a vasút és az ösvény?
Megoldás
Ha egyszer megyünk át, akkor a patak túloldalára jutunk, ha kétszer, akkor újra az eredeti oldalán leszünk. Tehát minden második átkelés után jutunk vissza az eredeti oldalra, így, ha nyolcszor megyünk át, akkor az eredeti oldalán maradunk. Vagyis a túra végén is balra lesz tőlünk a patak.
A vasutat ötször kereszteztük, ott éppen a másik oldalra kerülünk, a túra végén a vasút tőlünk jobbra lesz. Tehát a túra végi sorrend: patak, ösvény, vasút.
Ugráljunk!
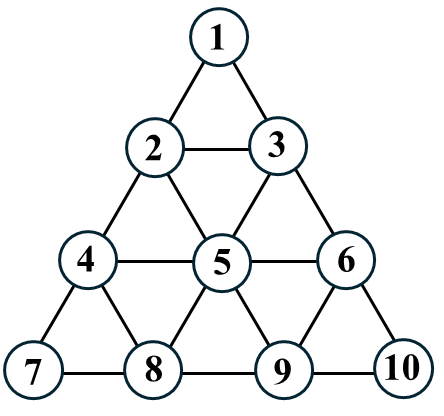
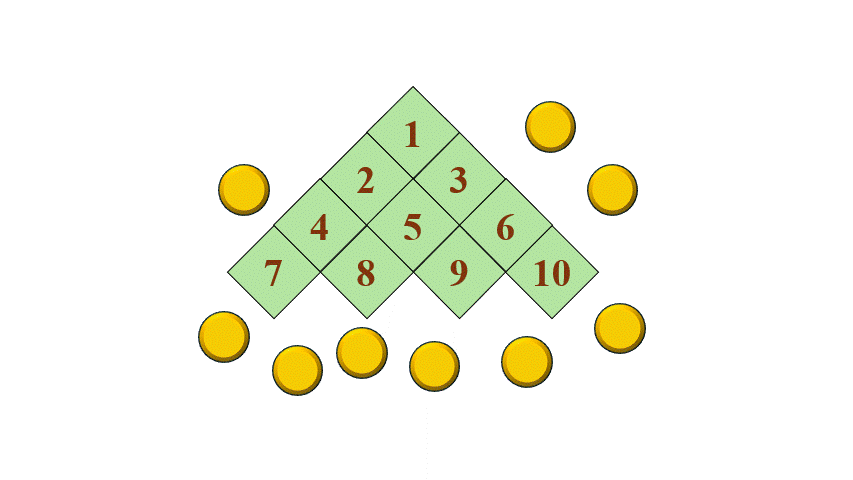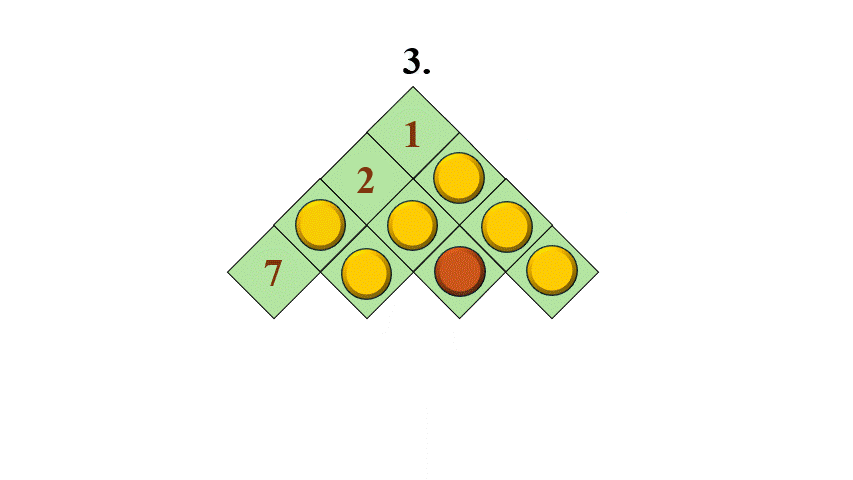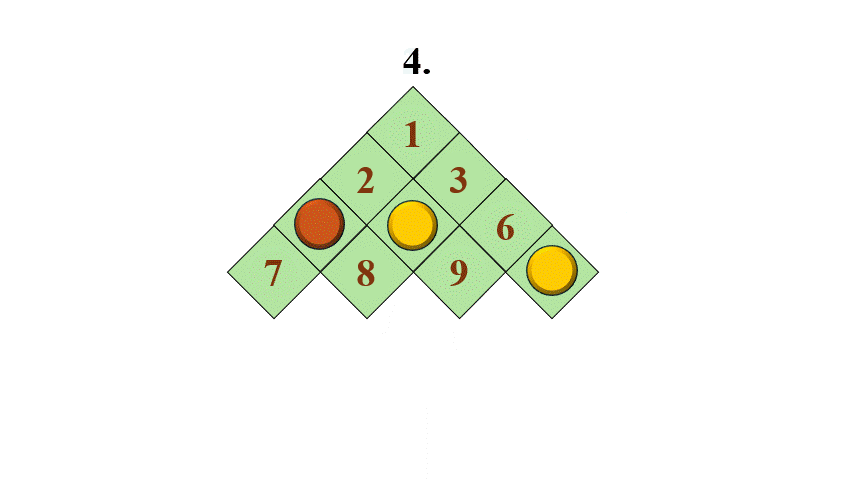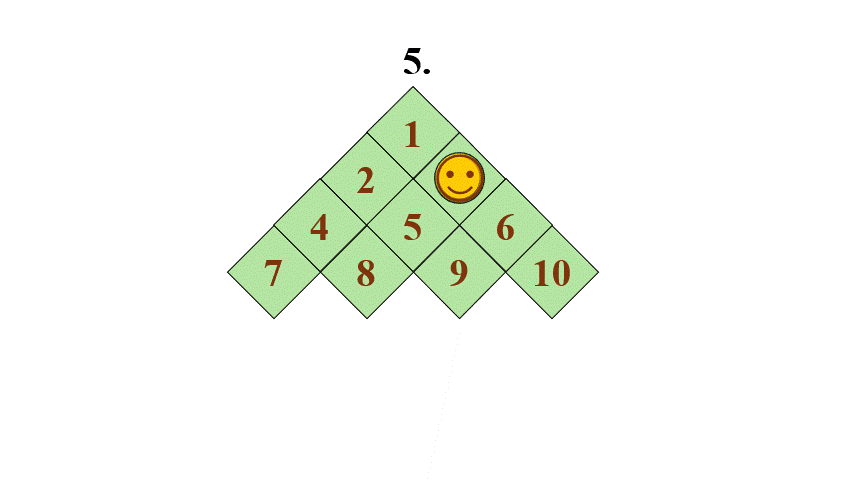
Rajzolj egy táblát (lásd alább), majd helyezz el kilenc bábut kilenc mezőn (gombot, cetlit)! A játék célja, hogy egy kivételével az összes bábut levegyük a tábláról.
Egy lépésben bármelyik bábuddal átugorhatsz egy szomszédos mezőn álló bábut, ami ezután lekerül a tábláról. Egy mezőn mindig csak egy bábu állhat! Szomszédosnak számít a közös oldalú vagy csúcsú mező, azaz 7-ről 9-re vagy 2-re is ugorhatsz. Más lépés nem lehetséges, minden ugrással le kell venned egy bábut. Ha egy kézbe vett bábuval tovább tudsz ugrani szabályosan egy következő üres mezőre, akkor ezt megteheted akárhányszor egymás után. Amíg el nem engeded a bábut, egy lépéssorozatnak számítanak a lépéseid.
Ha sikerült ügyesen elhelyezned, majd szabályos lépésekkel (egy híján) leszedegetned a bábukat, akkor elégedett lehetsz :) Ezután azon is érdekes lehet elgondolkodni, hogy meg tudod-e ezt tenni kevesebb lépéssorozattal is. Próbáld minél kevesebb sorozattal megvalósítani a bábuk leszedését!
Megoldás
5 lépéssorral levehető nyolc bábu. Célunk eléréséhez érdemes megfigyelni a tábla szerkezetét, ami valójában forgásszimmetrikus. Első ránézésre nem szembetűnő, de ha figyelembe vesszük a mezők elhelyezkedését és a lehetséges lépéseket, akkor már jól látszik, hogy megfeleltethető egy ilyen háromszögrácsnak:
No de térjünk vissza a táblához!
Érdemes elgondolkodni azon, hogy hogyan tudunk hosszabb lépéssorozatokat elérni. A 2-3-5 jó állásnak tűnik, mert egy ugrálással leszedegethető mindhárom bábu. 6-ról indulva ugyanide érünk vissza, és a következő ugrással erről a mezőről is leszedhető a bábu, ha a 10-es mezőn is van korong. (Máshonnan nézve a táblát ugyanennek az állásnak felel meg 5-6-7-8-9 vagy 4-5-8-9-10 is.)
Lássunk az előző gondolatok alapján egy lehetséges ötlépéses megoldást:
Hagyjuk szabadon a kettes mezőt a bábuk elhelyezésekor!
7→2
1→4
9→7→2
6→1→4→6
10→3
Ezt mutatja a következő animáció:
A tábla szerkezetéből adódóan a játék kezdetekor üresen hagyott mező a kettes helyett lehet a hármas, négyes, hatos, nyolcas vagy kilences is. Mindegyik a háromszög alakú tábla oldala mentén, nem csúcsban elhelyezkedő mező. Lépéseink könnyen átvihetők ezekre a kezdő helyzetekre.
Látható, hogy ha a középső (5) mezőt hagyjuk szabadon kezdő állapotként, akkor egyetlen bábu sem tud lépni.
Csúcsmezőt szabadon hagyva sem tudjuk megvalósítani célunkat. Ez viszonylag egyszerűen végigkövethető. Menet közben lesznek kötött lépések (ha figyelembe vesszük a forgásszimmetriát), lesznek elágazások, ahol többféle lépés közül választhatunk. Ezeket végignézve láthatjuk, hogy egyik ágon sem tudunk levenni nyolc korongot.






Ugráljunk!
Szabályos-e a 7 nyíl 8 nyíl 2 lépés a kezdö helyzetböl (vagyis amikor a 2 mezö marad üresen) , ezután levesszük a 8-as bábut?
Segítségek a mai feladatokhoz (a segítségeket erre a kommentre írom meg válaszul):